QBF Proofs and Certificates (Research Project)
Funding organization: Austrian Science Fund (FWF)
Project number: (ESP 197 ESPRIT-Programm)
Grant DOI: 10.55776/ESP197
Project Team
Leroy Chew (PI)
Topic
Quantified Boolean Formulas (QBF) extends propositional logic. Solving a QBF is theoretically more difficult than solving a propositional SAT (satisfiability) problem. QBFs are canonically PSPACE complete, meaning solving them could be used to solve any PSPACE problem by proxy. In the last decade progress in QBF solving is being undertaken. Proof complexity is the main theoretical framework used to understand SAT and QBF solving. Proof systems use the same logical rules as sound solvers, the proof size can often be a lower bound of running time between proof systems and related solvers. Proof systems can also be used to certify the correctness of solvers. However certification of QBF solvers is not yet a common occurrence.
We wish to further study the landscape of QBF proof complexity, studying the existing QBF proof systems that have emerged to capturing the solvers over the last decade. We also wish to use knowledge of soundness and complexity to make minor and major modifications to QBF proof systems, that could be beneficial to theory and practice. Our hope is that such knowledge will be of use to the QBF solving community.
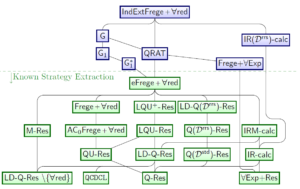
QBF proof systems arranged via p-simulation
Publications
Sorry, no results for this query- Leroy Chew, Tomáš Peitl. Better Extension Variables in DQBF via Independence. SAT 2025 [Preprint]
- Michael Hartisch, Leroy Chew. An Expansion-Based Approach for Quantified Integer Programming. Constraint Programming 2025 [Tool]
- Leroy Chew: Proof Simulation via Round-based Strategy Extraction for QBF. AAAI 2025 [Preprint][Proceedings][Tool]
- Leroy Chew, Alexis de Colnet, Stefan Szeider ASP-QRAT: A Conditionally Optimal Dual Proof System for ASP. KR2024[Proceedings]
- Sravanthi Chede, Leroy Chew, Anil Shukla: Circuits, Proofs and Propositional Model Counting. FSTTCS 2024 [Preprint][Proceedings]
- Leroy Chew, Alexis de Colnet, Friedrich Slivovsky, Stefan Szeider: Hardness of Random Reordered Encodings of Parity for Resolution and CDCL. AAAI 2024 [Preprint][Proceedings]
- Sravanthi Chede, Leroy Chew, Balesh Kumar, Anil Shukla: Understanding Nullstellensatz for QBFs. ECCC [Preprint]






