Two Sided Circular Layouts
Two-Sided Circular Layouts are a technique of enhancing circular graph drawings by finding a set of edges, which is then to be drawn in the outer face. On this website you find the code and test data used in the paper Minimizing Crossings in Constrained Two-Sided Circular Graph Layouts by Fabian Klute and Martin Nöllenburg, presented at SoCG'18 in Budapest.
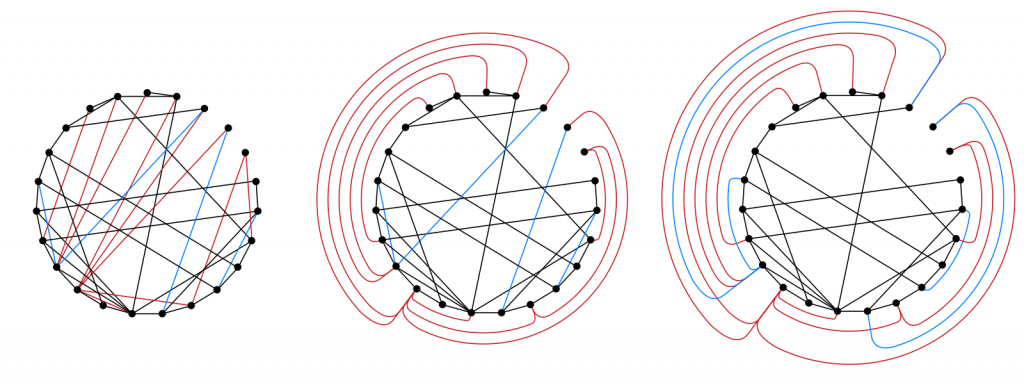
The here displayed pictures show, from left to right, a circular layout generated with OGDF, a two-sided layout with crossing free edges in the outer face and a two-sided layout with up to one crossing per edge in the outer face. The code is available in the following archive:
and the instances under:
The code comes with a qmake project file. The easiest way to build it is to use the QtCreator IDE.
From the paper:






