We count the number of preference profiles with voters and candidates , which are narcissistic and single-crossing (NSC) with respect to the order . This number is . We show this by establishing a bijective relation to semi-standard Young tableaux.
Each candidate appears in the top position of some voter once.
There is a linear order of the voters such that each pair of candidates divides the order into at most two suborders, where in each suborder, all voters have the same linear order on this pair.
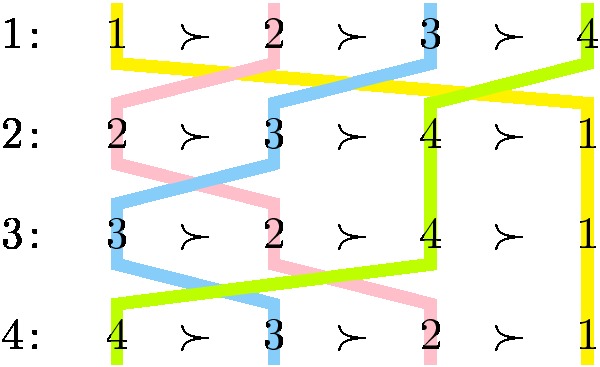
For each alternative, we draw a colored line, which passes through the same alternative in each voter’s preference order. It is easy to verify that each two colored lines cross at most once. This implies that the corresponding top-down order of the voters is a single-crossing order.
For a positive integer $n$, a semi-standard Young tableau (SSYT) of order consists of rows of positive integers that satisfy the following.
-
For each , the row contains entries with integers between and .
-
When aligned in the upper-left corner (to obtain an isosceles right triangle), the entries weakly increase along each row and strictly increase down each column.
| 1 | 1 | 1 |
| 2 | 3 | |
| 3 |
====================================
The paper is published in Discrete Mathematics and can be found here. You can also find an arxiv version here.
